Homework 9 (Local Move)
Up to the Phylogenetics main page
Larget-Simon Local Move
In this homework, you will take one step in a phylogenetic MCMC analysis by proposing, then accepting or rejecting, a Larget-Simon move. My main learning objective here is to reinforce several topics related to Bayesian phylogenetics covered in lecture so that you could, after completing the exercise, explain how programs like MrBayes and RevBayes propose (and accept or reject) steps in tree space in order to sample from the posterior distribution.
Here is an overview:
- You will be given a starting tree with edge lengths;
- Use PAUP* to compute the log-likelihood of this tree under the JC+G model using the data provided;
- Compute the log joint prior using an Exponential distribution with mean 0.1 for each edge length;
- Propose a new tree using the Larget-Simon proposal;
- Compute log-likelihood and log-joint-prior for the proposed tree;
- Compute the acceptance ratio to see whether the proposed tree should be accepted;
- Turn in answers to the questions in the “Worksheet” section of this assignment.
Pseudorandom numbers
This time you choose what seed to begin with. That way we will all get a slightly different answer.
Use this python3 script, substituting in your own favorite positive integer (e.g. 12345, your 5-digit zip code, your birth year, etc.) for the xxxxx:
from random import random,seed
seed(xxxxx)
for i in range(7):
u = random()
print(' u%d = %.5f' % (i,u))
I will refer to these 7 pseudorandom numbers by name; e.g. u0, u1, …, u6 (inside equations, these may look like \(u_1, u_2, \cdots, u_6\)).
Worksheet
Copy the questions below to a blank text file. As you follow the instructions below, record results in this “worksheet” as instructed, using 5 decimals precision when reporting numbers.
1. seed used when generating pseudorandom numbers
answer:
2. log-likelihood of the starting tree assuming shape = 0.3
answer:
3. log of the joint prior for the starting tree
answer:
4. log of the posterior kernel for the starting tree:
answer:
5. edge at the center of 3-edge segment:
answer:
6. left edge in 3-edge segment:
answer:
7. right edge in 3-edge segment:
answer:
8. scaling factor m:
answer:
9. subtree to move:
answer:
10. newick description of proposed tree with edge lengths
answer:
11. log-likelihood of the proposed tree assuming shape = 0.3:
answer:
12. log of the joint prior for the proposed tree:
answer:
13. log of the posterior kernel for the proposed tree:
answer:
14. log of the acceptance ratio:
answer:
15. log of the Hastings ratio:
answer:
16. log of the acceptance probability:
answer:
17. decision (accept or reject):
answer:
Data set
Download this dataset to use when computing likelihoods: green5.nex
Starting tree
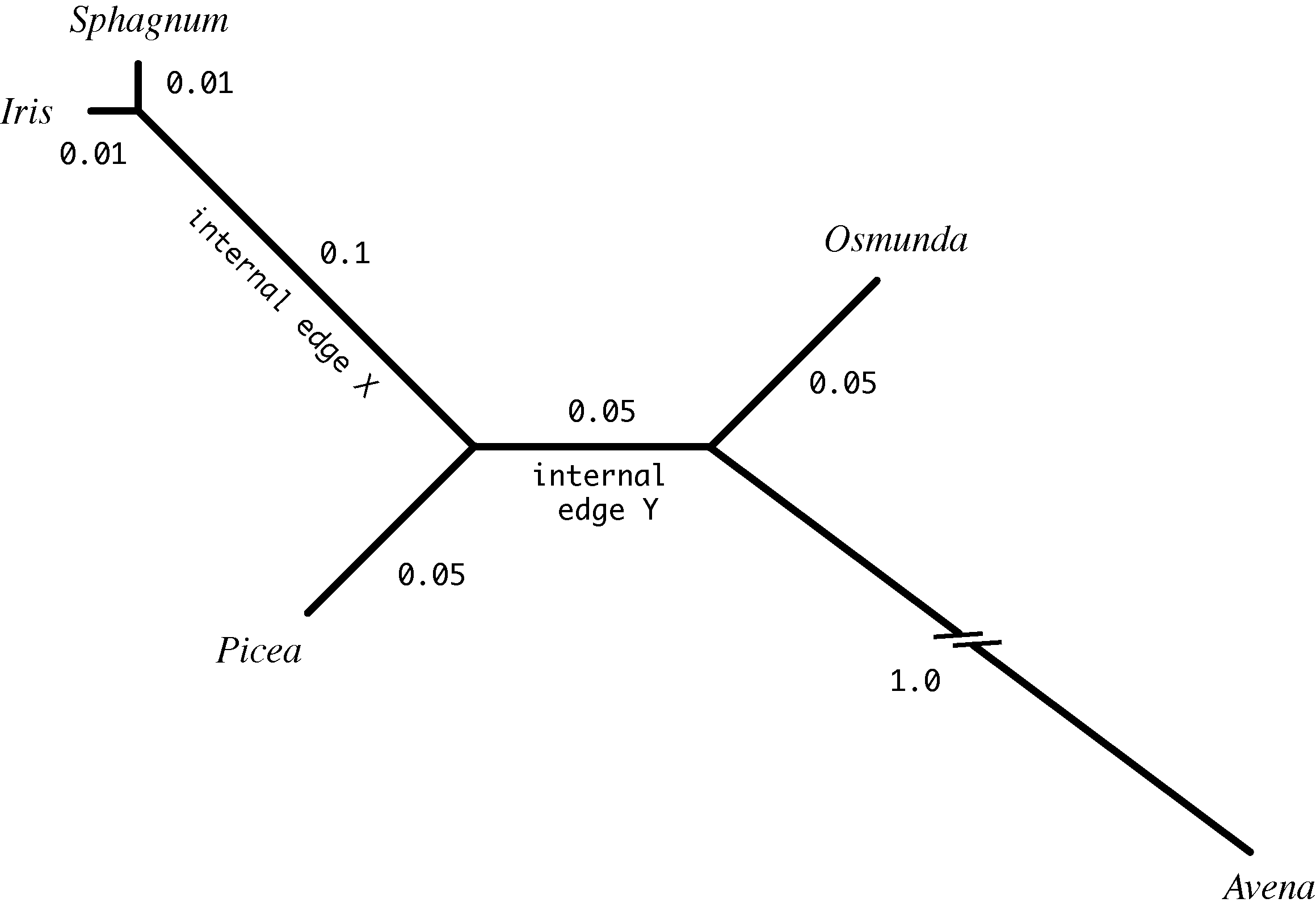
Important: See the “Hints” section near the bottom of this web page before completing this section!
Compute the log-likelihood (using PAUP*, JC69+G model, shape fixed at 0.3) as well as the log joint Exponential(10) prior and record these values along with the log posterior kernel (log likelihood + log joint prior) on the worksheet.
If you’ve forgotten how to set up PAUP* to compute likelihoods, revisit the likelihood lab.
Choosing a 3-edge segment at random
First choose an internal edge at random. There are two internal edges (labeled X and Y in the figure above) so use your first random number u0 to decide (u0 < 0.5, choose X, otherwise choose Y).
Now choose one of the two branches at the left end of your chosen internal edge as the 2nd edge in your 3-edge segment.
-
If you chose internal edge X, then choose the Iris edge if u1 < 0.5, otherwise choose the Sphagnum edge.
-
If you chose internal edge Y, then choose the Picea edge if u1 < 0.5, otherwise choose the (Iris,Sphagnum) edge.
Finally choose one of the two branches at the right end of your chosen internal edge as the 3rd edge in your 3-edge segment.
-
If you chose internal edge X, then choose the (Osmunda,Avena) edge if u2 < 0.5, otherwise choose the Picea edge.
-
If you chose internal edge Y, then choose the Osmunda edge if u2 < 0.5, otherwise choose the (Avena) edge.
Record your choices in the worksheet.
Modify the length of your 3-edge segment
Calculate a scaling factor \(m\) using the following formula:
\[m = e^{u_3 - 0.5}\]Note that you will use your fourth random number (u3) for this. Here is how \(m\) would be computed in python:
import math
m = math.exp(u3 - 0.5)
Record the value of \(m\) in the worksheet.
Before moving to the next step, multiply each of the three edges (left, central, and right) in your 3-edge segment by \(m\). This will have the effect of either expanding (if \(m > 1\)) or contracting (if \(m<1\)) your 3-edge segment in the proposed tree.
Choose subtree to move
Use u4 to choose which subtree (left or right) to move. If u4 < 0.5, then move the subtree on the left; otherwise move the subtree on the right. What do I mean by left/right subtree? Your 3-edge segment has two “elbows”, or branching points. At each of these elbows (left or right), 2 of the edges are part of your 3-edge segment. The 3rd edge (not part of your 3-edge segment) is the one you would move if chosen using u4.
For example, if your 3-edge segment is Iris (left), X (center), and Picea (right), then the subtree to move would be Sphagnum if u4 < 0.5 or (Osmunda,Avena) if u4 >= 0.5.
Record which subtree you chose in the worksheet.
Move the chosen subtree
Use u5 to choose where to place the subtree you chose to move. Multiply u5 times the length of your proposed 3-edge segment to produce the value \(z\). (By proposed 3-edge segment I mean the lengths of the 3 edges after multiplying by the scaling factor \(m\)). Starting at the leftmost end of your 3-edge segment, travel left to right along your three edge segment until you’ve used up an amount of edge length equal to \(z\).
For example, if your 3-edge segment is Iris (left), X (center), and Picea (right) and \(m=0.7\), then the proposed lengths of the 3 edges would be 0.007 (left), 0.07 (center), and 0.035 (right). The total length of the proposed 3-edge segment is 0.112. If \(u_4=0.4\), \(z=(0.4)(0.112)=0.0448\). The value of \(z\) is longer than the leftmost edge (0.007) in your proposed 3-edge segment, but not as large as the combined lengths of the left and center edges (0.077), so you would place your detached subtree at a point \(0.0448 - 0.007 = 0.0378\) from the left end of the central edge (i.e. internal edge X).
Create a newick tree description with edge lengths and record in the worksheet. Note: you will need to create this newick tree description in order to have PAUP* calculate the log likelihood of the proposed tree.
Calculate the log-kernel for the proposed tree
Create a nexus file that, when executed in PAUP, computes the log-likelihood of the proposed tree. Use the JC+G model again with fixed shape = 0.3. Be sure to specify userbrlens when computing the log-likelihood so that PAUP will not try to estimate edge lengths.
Recompute the log joint prior using the modified edge lengths.
Record the log-likelihood, the log joint prior, and the sum of these two numbers (log kernel) for the proposed tree in the worksheet.
Compute the acceptance probability
The last step is to decide whether to accept the proposed tree. For this you will use your last remaining random number u6.
The acceptance probability for this move (proposal) is
\[\mbox{acceptance prob.} = \min\left\{ 1, \left( \frac{p(D|\theta^{\ast}) p(\theta^{\ast})}{p(D|\theta) p(\theta)} \right) m^3 \right\},\]where \(\theta\) represents the starting tree (topology and edge lengths), \(\theta^{\ast}\) represents the proposed tree (topology and edge lengths), and \(m^3\) is the Hastings ratio (the ratio of the probability of the reverse move to the probability of the forward move). The calculation of the Hastings ratio for this move is described in detail in Holder et al. (2005), but here we will skip the details of how it is determined and just use the result.
First compute the log of acceptance ratio \(R\). \(\log(R)\) equals the log of the proposed posterior kernel minus the log of the starting tree posterior kernel. Now compute the log of the Hastings ratio (the Larget-Simon local move is not symmetric). The Hastings ratio is \(m^3\), which, on the log scale, is $3 \log(m)$. Adding the log Hastings ratio to \(\log(R)\) yields the log of the acceptance probability. If this value is greater than 0.0, then set it equal to 0.0 (because probabilities cannot be greater than 1.0, and thus the log of a probability cannot be greater than 0.0).
It is simplest to just keep everything on log scale, so compute the natural logarithm of u6 for comparison with your acceptance probability, which is already on log scale. If the log of u6 is less than your log acceptance probability, then you would accept the proposed tree. If the log of u6 is greater than or equal to the log of the acceptance probability, then you would reject the proposed tree.
Record your log Hastings ratio, log acceptance ratio, and your decision (accept or reject) in the worksheet.
You’re done!
Hints
Be sure PAUP’s output contains these 3 lines (not necessarily together) when you are computing the log likelihood (just a check to make sure you have PAUP set up correctly):
Rates at variable sites = gamma, shape=0.3 (4 categories [mean])
Model correspondence = JC69+G
Branch lengths constrained to user-input values
To make PAUP* report log-likelihoods with 5 decimals precision, use the scoredigits setting in lset, which determines the total number of digits used in reporting the score. Note that we must set scoredigits to 9 because the likelihood score contains 4 digits to the left of the decimal point. The ellipses (…) in the example below stands for the other things you will need to specify in your lset command, such as nst, basefreq, rates, and shape.
lset ... scoredigits=9;
An Exponential(\(\lambda\)) distribution having rate \(\lambda\) and mean \(1/\lambda\) has probability density function \(p(v|\lambda) = \lambda e^{-\lambda v}\), where \(v\) is a particular edge length.
The log of an Exponential(\(\lambda\)) distribution is \(\log p(v|\lambda) = \log \lambda - \lambda v\).
The joint prior in this exercise is the product of 8 quantities: the tree topology prior and the prior densities for all 7 edge lengths. The log of the joint prior is thus a sum of 8 quantities: the log of the tree topology prior and the log prior densities for all 7 edge lengths.
The tree topology prior is discrete uniform and the number of possible unrooted tree topologies for 5 taxa is 15, so the prior probability of any particular tree topology is 1/15 (and the log prior probability for any particular tree topology is \(\log(1) - \log(15) = 0 - \log(15) = -\log(15)\).
Note that we do not need to include a prior for the shape parameter because it is fixed at 0.3. You only include priors for parameters that are free to vary in your model.
What to turn in
Turn in your worksheet on Slack (preferably), email, or via printout in class.
answer: