RevBayes Divergence Dating Lab

Goals

The goal of this lab exercise is to introduce you to Bayesian divergence time estimation. There are other programs that are popular for divergence time analyses (notably BEAST2), but we will use RevBayes because you already have some experience with this program (namely the RevBayes lab).

Answer template

Here is a text file template in which to store your answers to the thinking questions:

1. What is the 95% HPD (highest posterior density) credible interval for clock_rate (use the Estimates tab in Tracer to find this information)? Does this include the true value? 
answer:

2. What is the 95% HPD (highest posterior density) credible interval for birth_rate? Does this include the true value?
answer:
    
3. Which parameter (clock_rate or birth_rate) is hardest to estimate precisely (i.e. has the broadest HPD credible interval)? 
answer:

4. For the parameter you identified in the previous question, would it help to simulate 20000 sites rather than 10000? 
answer:

5. What would help in reducing the HPD interval for birth_rate? 
answer:

6. Using the Marginal Density tab in Tracer, select all 6 exchangeabilities. What do these values represent, and what about these densities makes sense given what you know about the true model used to simulate the data? 
answer:

7. Using the Marginal Density tab in Tracer, select all 4 state_freqs. What about these densities make sense given what you know about the true model used to simulate the data?
answer:

8. What is the true rate for any given edge in the tree?
answer:

9. Looking across the 38 branch rate parameters, do any of them get very far from 1.0 (e.g. less than 0.98 or greater than 1.2)? 
answer:

10. What are the mean values of ucln_mu and ucln_sigma, our two hyperparameters that govern the assumed lognormal prior applied to each branch rate? 
answer:

11. What do these values translate to on the linear scale (use the formulas in the figure from lecture to do the calculation)?
answer:

12. Do the values on the linear scale make sense in light of the fact that you know that the data were simulated under a strict clock with rate 1.0?
answer:

13. We've added moves, but no parameters or priors for the node times. Why not?
answer:

14. Does the MAP tree have the same topology as the true tree
answer:

15. Are we more confident about recent nodes or ancient nodes in the tree?
answer:

16. What would you conclude if these credible intervals were exactly the same size if we had performed the MCMC analysis on the prior only, with no data?
answer:

17. Does the data contain information about substitution rates?
answer:

Getting started

srun --qos=mcbstudent --partition=mcbstudent --mem=5G --pty bash

to start a session on a node that is not currently running jobs.

Important The --mem=5G part is important for this lab, as RevBayes uses more than the default amount (128 MB) of memory sometimes.

Create a directory

Use the unix mkdir command to create a directory to play in today:

cd
mkdir rbdiv

Load the RevBayes module

You will need to load the RevBayes/1.1.1 module in order to use RevBayes:

module load RevBayes/1.1.1

Load the PAML module

You will need to load the paml/4.9 module in order to use PAML, which we will use to simulate data:

module load paml/4.9

Simulating and analyzing under the strict clock model

Divergence time analyses are the trickiest type of analysis we will do in this course. That’s because the sequences do not contain information about substitution rates or divergence times per se; they contain information about the number of substitutions that have occurred, and the number of substitutions is the product of rate and time. Thus, maximum likelihood methods cannot separate rates from times; doing so requires a Bayesian approach and considered use of priors, which constrain the range of rate and time scenarios considered plausible.

We will thus start slowly, and we will simulate data so that we know the truth. This will help guide your expectations when conducting divergence time analyses on real data.

PAML evolver

Let’s use the evolver program, which is part of Ziheng Yang’s PAML package, to simulate data for 10000 sites on a 20-taxon pure birth (Yule) tree using a strict clock. This will allow us to know everything: the birth rate of the tree generating process, the clock rate (i.e. the substitution rate that applies to the entire tree), as well as the model used for simulation.

We will each use a different random number seed, so we should all get slightly different answers.

Simulate a tree

First simulate a pure birth tree using evolver. Start evolver by simply typing evolver at the bash prompt, then enter the information provided below at the prompts (for questions that ask for multiple quantities, just separate the values by a space):

specify that you want to generate a rooted tree by typing 2
specify 20 species
specify 1 tree and a random number seed of your choosing (separate these two positive whole numbers with a space)
specify 1 to answer yes to the question about wanting branch lengths
specify 2.6 for the birth rate, 0.0 for the death rate, 1.0 for the sampling fraction, and 1.0 for the tree height (separate these numbers with at least one space; e.g. “2.6 0.0 1.0 1.0”
press 0 to quit

One thing to note before we continue. PAML’s evolver program scales the tree to have height equal to the specified mutation rate (1.0, the last number we specified above). Normally pure birth trees would have different heights because of stochastic variation, but apparently this is only possible in evolver by editing the source code and making your own ad hoc version. I’ve done the next best thing, which is set the birth rate to the value (2.6) that yields a tree having expected height 1.0.

You should now find a tree description in the file evolver.out. Rename this file tree.txt (this will prevent your tree description from being overwritten when you run evolver again, and we will use the tree.txt file as input to RevBayes):

mv evolver.out tree.txt

Simulate sequences

The PAML evolver program requires a control file specifying everything it needs to know to perform your simulation. Create a file named control.dat with the following contents (note: 2 lines require modification: seed and tree description):

2
seed goes here
20 10000 1
-1
tree description goes here
4 
5
0 0 
0.1 0.2 0.3 0.4

Here’s what each of those lines does (consult the evolver section of the PAML manual for more info about each option):

line 1: 2 specifies that we want the output as a nexus file
line 2: you should enter your own random number seed on the second line (can be the same as the one you used for the tree)
line 3: 20 taxa, 10000 sites, 1 data set
line 4: -1 says to use the branch lengths in the tree description
line 5: tree description: paste in the tree description you generated from the first evolve run here
line 6: 4 specifies the HKY model
line 7: set kappa equal to 5
line 8: set the gamma shape parameter to 0 and the number of rate categories to 0 (i.e. no rate heterogeneity)
line 9: set state frequencies to: T=0.1, C=0.2, A=0.3, and G=0.4 (note, not in alphabetical order!)

When saving simulated data in nexus format, PAML’s evolver command looks for three files (paupstart, paupend, and paupblock) specifying what text should go at the beginning, end, and following each data matrix generated, respectively. The only one of these files that needs to have anything in it is paupstart.

Here’s the quick way to create these files:

echo "#nexus" > paupstart
touch paupblock
touch paupend

The echo command parrots what you put in quotes and the > paupstart at the end creates the file paupstart and saves the echoed contents there (you could use >> paupstart if you wanted to append other lines to the file).

The touch command is intended to update the time stamp on a file, but will create an empty text file if the file specified does not exist.

Run evolver now using this control file, and selecting option (5) from the menu, which is “Simulate nucleotide data sets”.

evolver 5 control.dat

If you get Error: err tree… it means that you did not follow the directions above ;)

You should now find a file named mc.nex containing the sequence data.

Use RevBayes to estimate the birth rate and clock rate

In our first RevBayes analysis, we will see how well we can estimate what we already know to be true about the evolution of both the tree and the sequences. You will cheat and fix some things to their known true values, such as the tree topology and edge lengths. The idea is to take small steps so that we know what we are doing all along.

As you already know from previous labs, RevBayes uses an R-like language called the Rev Language to specify the model and the analysis. Rev is not R, but it is so similar to R that you will often forget that you are not using R and will try things that work in R but do not work in Rev - just a heads-up!

Set up the tree submodel

Create a new file named strict.Rev and add the following to it: I’ll provide some explanation below the code block.

# Load data and tree

D <- readDiscreteCharacterData(file="mc.nex")
n_sites <- D.nchar()

T <- readTrees("tree.txt")[1]
n_taxa  <- T.ntips()
taxa  <- T.taxa()

# Initialize move (nmoves) and monitor (nmonitors) counters

nmoves = 1
nmonitors = 1

# Birth-death tree model

death_rate <- 0.0
birth_rate ~ dnExponential(0.01)
birth_rate.setValue(1.0)
diversification := birth_rate - death_rate
moves[nmoves++] = mvSlide(birth_rate, delta=1.0, tune=true, tuneTarget=0.4, weight=1.0)
sampling_fraction <- 1.0
root_time <- T.rootAge()
timetree ~ dnBDP(lambda = birth_rate, 
    mu = death_rate, 
    rho = sampling_fraction, 
    rootAge = root_time, 
    samplingStrategy = "uniform", 
    condition = "nTaxa", 
    taxa = taxa)
timetree.setValue(T)

Note that we are assigning only the first tree in trees.txt to the variable T (there is only 1 tree in that file, but RevBayes stores the trees it reads in a vector, so you have to add the [1] to select the first anyway).

The functions beginning with dn (e.g. dnExponential and dnBDP) are probability distributions. Thus, birth_rate is a parameter that is assigned an Exponential prior distribution having rate 0.01, and timetree is a compound parameter representing the tree and its branching times that is assigned a Birth Death Process (BDP) prior distribution. The BDP is a submodel, like the +I or +G rate heterogeneity submodels: it has its own parameters (lambda, mu, rho, and rootAge) all of which are fixed except for birth_rate.

The setValue function used on the last line sets the starting value of a parameter that is allowed to vary. In this case, we are using setValue to start off our MCMC analysis with the true tree and true edge lengths.

Each parameter in the model requires a mechanism to propose changes to its value during an MCMC run. These are called moves. A vector of moves has been created for you, so you need only add to it. The variable nmoves keeps track of how many moves we’ve defined. Each time a move is added to the moves vector, we increment the variable nmoves so that new moves will not overwrite previously defined moves. This increment is performed by the ++ in nmoves++. Thus, if nmoves currently has the value 2, moves[nmoves++] = ... sets the value of moves[2] to ... (not literally, of course; the ellipses stand in for whatever move you are creating) and immediately increments nmoves to 3 so it will refer to the next empty slot in the moves vector whenever we add another move.

Monitors in RevBayes handle output. We are just initializing the monitor counters now; we will add monitors toward the end of our RevBayes script.

The model can be summarized by a DAG (Directed Acyclic Graph). The nodes of this graph are of several types and represent model inputs and outputs:

Stochastic nodes are exemplified by birth_rate and timetree; they can be identified by the tilde (~) symbol used to assign a prior distribution. These quantities are parameters that will be updated during MCMC.
Constant nodes are exemplified by death_rate, sampling_fraction, and root_time; they can be identified by the assignment operator <- that fixes their value to a constant. They are not changed during the MCMC analysis.
Deterministic nodes are exemplified by diversification; they can be identified by the assignment operator :=. These nodes represent functions of other nodes used to output quantities in a more understandable way. For example, diversification (birth rate minus death rate) will show up as a column in the output even though it is not a parameter of the model itself. (The diversification node was only added here to illustrate deterministic nodes; it’s value will always equal birth_rate because death_rate is a constant 0.0).

Set up the strict clock submodel

Add the following 3 lines to your growing strict.Rev file:

# Strict clock

clock_rate ~ dnExponential(0.01)
clock_rate.setValue(1.0) 
moves[nmoves++] = mvSlide(clock_rate, delta=1.0, tune=true, tuneTarget=0.4, weight=1.0)

This adds a parameter clock_rate with a vague Exponential prior (rate 0.01) and starting value 1.0. The move we’re using to propose new values for this parameter as well as the birth_rate parameter is a sliding window move, which you are familiar with from your MCMC homework. The value delta is the width of the window centered over the current value, and we’ve told RevBayes to tune this proposal during the burnin period so that it achieves (if possible) an acceptance rate of 40%. The weight determines the probability that this move will be tried. At the start of the MCMC analysis, RevBayes sums the weights of all moves you’ve defined and uses the weight divided by the sum of all weights as the probability of selecting that particular move next.

Set up the substitution submodel

Now let’s set up a GTR substitution model:

# GTR model

state_freqs ~ dnDirichlet(v(1,1,1,1))
exchangeabilities ~ dnDirichlet(v(1,1,1,1,1,1))
Q := fnGTR(exchangeabilities, state_freqs)
moves[nmoves++] = mvDirichletSimplex(exchangeabilities, alpha=10.0, tune=true, weight=1.0)
moves[nmoves++] = mvDirichletSimplex(state_freqs, alpha=10.0, tune=true, weight=1.0)

The Q matrix for the GTR model involves state frequencies and exchangeabilities. I’ve made both state_freqs and exchangeabilities stochastic nodes in our DAG and assigned both of them flat Dirichlet prior distributions (the v(1,1,...,1) part is the vector of parameters for the Dirichlet prior distribution (all 1s produces a flat prior distribution in which every possible combination of state frequencies (or exchangeabilities) is equally probable).

I’ve assigned mvDirichletSimplex moves to both of these parameters. A simplex is a set of coordinates that are constrained to sum to 1, and this proposal mechanism modifies all of the state frequencies (or exchangeabilities) simultaneously while preserving this constraint. A list of all available moves can be found in the Documentation section of the RevBayes web site if you want to know more.

Finalize the PhyloCTMC

It is time to collect the various submodels (timetree, Q, and clock_rate) into one big Phylogenetic Continuous Time Markov Chain (dnPhyloCTMC) distribution object and attach (clamp) the data matrix D to it.

# PhyloCTMC

phySeq ~ dnPhyloCTMC(tree=timetree, Q=Q, branchRates=clock_rate, nSites=n_sites, type="DNA")
phySeq.clamp(D)
mymodel = model(exchangeabilities)

The last line above is a little obscure. RevBayes needs to have an entry point (a root node, if you will) into the DAG, and any stochastic node will suffice. Here I’ve supplied exchangeabilities when constructing mymodel, but I could have instead provided state_freqs, birth_rate, clock_rate, or any other variable representing a node in the DAG.

Add one more line to this section of your file:

mymodel.graph("strict.dot", TRUE, "white")

This line creates a file named strict.dot that contains code (in the dot language) for creating a plot of your DAG. The second argument (TRUE) tells the graph command to be verbose, and the last argument (“white”) specifies the background color for the plot.

Set up monitors

Let’s create 2 monitors to keep track of sampled parameter values, sampled trees, and screen output:

# Monitors

monitors[nmonitors++] = mnModel(filename  = "output/strict.log",  printgen = 10, separator = TAB) 
monitors[nmonitors++] = mnFile(filename  = "output/strict.trees", printgen = 10, timetree)
monitors[nmonitors++] = mnScreen(printgen=100)

The first monitor will save model parameter values to a file named strict.log in the output directory (which will be created if necessary). The second monitor will save trees to a file named strict.trees in the output directory. Note that we have to give it timetree as an argument. This is kind of silly because we’ve fixed the tree topology and edge lengths, so all the lines in the strict.trees will be identical, but let’s add it anyway just as a sanity check to verify that the tree topology and edge lengths don’t change during the MCMC run. Finally, the third monitor produces output to the console so that you can monitor progress.

Note that we are sampling only every 10th iteration for the first 2 monitors and every 100th iteration for the screen monitor.

Set up MCMC

Finally, we’re ready to add the final section to our revscript. Here we create an mcmc object that combines the model, monitors, and moves and says to do just 1 MCMC analysis. We will devote the first 1000 iterations to burnin, stopping to tune the moves every 100 iterations (RevBayes collects data for 100 iterations to compute the acceptance probabilities for each move, then uses that to decide whether to make the move bolder or more conservative.) Then we run for real for 10000 iterations and ask RevBayes to output an operator summary, which will tell us how often each of our moves was attempted and succeeded.

# MCMC

mymcmc = mcmc(mymodel, monitors, moves, nruns=1)
mymcmc.burnin(generations=1000, tuningInterval=100)
mymcmc.run(generations=10000)
mymcmc.operatorSummary()

quit()

Run RevBayes

To run RevBayes, enter the following at the command prompt with the name of your revscript file last:

rb strict.Rev

If this were a long analysis, we would create a slurm script and submit the job using sbatch, but this one should be short enough that you can easily wait for it to finish while logged in.

Reviewing the strict clock results

First, copy the contents of the file strict.dot and paste them into one of the online Graphviz viewers such as GraphvizFiddle, GraphvizOnline, or WebGraphviz. The resulting plot shows your entire model as a graph, with constant nodes in square boxes, stochastic nodes in solid-line ovals, and deterministic nodes in dotted-line ovals.

Now download the file strict.log stored in the output directory to your laptop and open it in Tracer.

What is the 95% HPD (highest posterior density) credible interval for clock_rate (use the Estimates tab in Tracer to find this information)? Does this include the true value?

What is the 95% HPD (highest posterior density) credible interval for birth_rate? Does this include the true value?

Which parameter (clock_rate or birth_rate) is hardest to estimate precisely (i.e. has the broadest HPD credible interval)?

For the parameter you identified in the previous question, would it help to simulate 20000 sites rather than 10000?

What would help in reducing the HPD interval for birth_rate?

Using the Marginal Density tab in Tracer, select all 6 exchangeabilities. What do these values represent, and what about these densities makes sense given what you know about the true model used to simulate the data?

Using the Marginal Density tab in Tracer, select all 4 state_freqs. What about these densities make sense given what you know about the true model used to simulate the data?

You may have noticed that our effective sample sizes for the exchangeabilities and state_freqs parameters are pretty low. You no doubt also noticed that these are being estimated quite precisely and accurately. What gives? The fact that there is so much information in the data about these parameters is the problem here. The densities for these parameters are very sharp (low variance), and proposals that move the values for these parameters away from the optimum by very much fail. Looking at the operator summary table generated after the MCMC analysis finished, you will notice that RevBayes maxed out its tuning parameter (alpha) for both exchangeabilities and state_freqs at 100. Making this tuning parameter larger results in smaller proposed changes, so if we could set the tuning parameter alpha to, say, 1000 or even 10000, we could achieve better acceptance rates and higher ESSs.

Relaxed clocks

It is safe to assume that a strict molecular clock almost never applies to real data. So, it would be good to allow some flexibility in rates. One common approach is to assume that the rates for each edge are drawn from a lognormal distribution. This is often called an UnCorrelated Lognormal (UCLN) relaxed clock model because the rate for each edge is independent of the rate for all other edges (that’s the uncorrelated part) and all rates are lognormally distributed. This is to distinguish this approach from correlated relaxed clock models, which assume that rates are to some extent inherited from ancestors, and thus there is autocorrelation across the tree.

Copy your strict.Rev script to a file named relaxed.Rev:

cp strict.Rev relaxed.Rev

Edit relaxed.Rev, replacing the section entitled “Strict clock” with this relaxed clock version:

# Uncorrelated Lognormal relaxed clock

# Add hyperparameters mu and sigma
ucln_mu ~ dnNormal(0.0, 100)
ucln_sigma ~ dnExponential(.01)
moves[nmoves++] = mvSlide(ucln_mu,    delta=0.5, tune=true, tuneTarget=0.4, weight=1.0)
moves[nmoves++] = mvSlide(ucln_sigma, delta=0.5, tune=true, tuneTarget=0.4, weight=1.0)

# Create a vector of stochastic nodes representing branch rate parameters
n_branches <- 2*n_taxa - 2
for(i in 1:n_branches) {
    branch_rates[i] ~ dnLognormal(ucln_mu, ucln_sigma)
    branch_rates[i].setValue(1.0)
    moves[nmoves++] = mvSlide(branch_rates[i], delta=0.5, tune=true, weight=1.0)
}

You’ll also need to substitute branch_rates for clock_rate in your dnPhyloCTMC call:

phySeq ~ dnPhyloCTMC(tree=timetree, Q=Q, branchRates=branch_rates, nSites=n_sites, type="DNA")

The model has suddenly gotten a lot more complicated, hasn’t it? We now have a rate parameter for every edge in the tree, so we’ve added \((2)(20) - 2 = 38\) more parameters to the model. Each of these edge rate parameters has a lognormal prior, and the 2 parameters of that distribution represent hyperparameters in what is now a hierarchical model, so we’ve increased the model from 10 parameters (1 clock_rate, 1 birth_rate, 3 state_freqs, 5 exchangeabilities) to 50 parameters (the original 10 plus 38 edge rates and 2 hyperparameters ucln_mu and ucln_sigma).

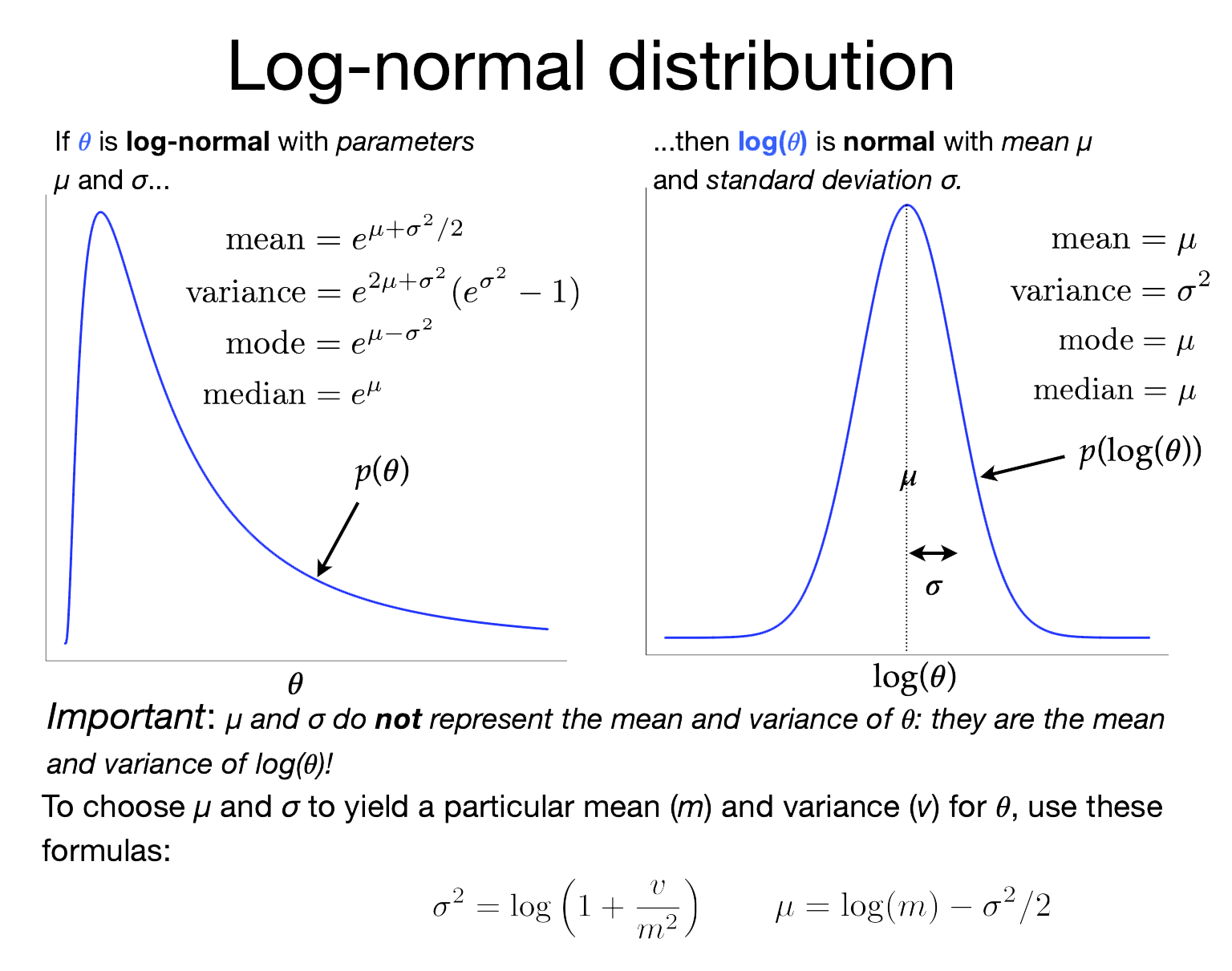
To the right is slide 5 from the March 5, 2024, lecture that shows the relationship between the lognormal distribution (left) and the normal distribution (right). The lognormal distribution is tricky in that its two parameters (\(\mu\) and \(\sigma\)) are not the mean and standard deviation of the lognormally-distributed variable, as you might be led to assume if you are used to the \(\mu\) and \(\sigma\) associated with normal distributions. In a Lognormal distribution, \(\mu\) and \(\sigma\) are, instead, the mean and standard deviation of the log of the lognormally-distributed variable!

Note this line:

branch_rates[i].setValue(1.0)

This sets the starting value of all branch rate parameters to 1.

This seems to be kind of important. If you let RevBayes choose starting values for branch rates, it will start by drawing values for hyperparameters ucln_mu and ucln_sigma (which, due to the high variances we’ve given to their hyperpriors, can result in some pretty crazy values) and then will draw values from Lognormal(ucln_mu, ucln_sigma) to serve as starting values for the branch rates. This procedure could start us very far away from a reasonable constellation of parameter values and the MCMC analysis may never find its way to a reasonable configuration, at least with the length of run we are able to manage in a lab period.

Unless you are particularly interested in how well your MCMC converges from diverse starting points, it is a good idea to start an MCMC analysis with all parameters set to reasonable values, for example maximum likelihood estimates (MLEs). This does not violate Bayesian principles in any way, and it saves on the amount of burnin that needs to be done. This is especially true for complex models where the amount of information for estimating parameters is low. Here I’m cheating a bit and setting the branch rates to what I know is the true value (1.0), but if we used our estimated clock_rate from the previous analysis things would work out just as well.

You should also edit the monitors section so that the output file names reflect the fact that we’re using a relaxed clock now:

# Monitors

monitors[nmonitors++] = mnModel(filename  = "output/relaxed.log",  printgen = 10, separator = TAB) 
monitors[nmonitors++] = mnFile(filename  = "output/relaxed.trees", printgen = 10, timetree)
monitors[nmonitors++] = mnScreen(printgen=100)

And don’t forget to change the name of the dot file:

mymodel.graph("relaxed.dot", TRUE, "white")

Now run the new model:

rb relaxed.Rev

Review results of the relaxed clock analysis

If you create a plot of your relaxed.dot file using one of the online Graphviz viewers, the increase in model complexity will be very apparent!

Open the relaxed.log file in Tracer and answer the following questions:

What is the true rate for any given edge in the tree?

Looking across the 38 branch rate parameters, do any of them get very far from 1.0 (e.g. less than 0.98 or greater than 1.2)?

What are the mean values of ucln_mu and ucln_sigma, our two hyperparameters that govern the assumed lognormal prior applied to each branch rate?

What do these values translate to on the linear scale (use the formulas in the figure from lecture to do the calculation)?

Do the values on the linear scale make sense in light of the fact that you know that the data were simulated under a strict clock with rate 1.0?

Divergence times

So far we’ve not estimated divergence times; we’ve assumed the true tree topology and true divergence times for all of our analyses. In reality, our main interest probably lies in estimating divergence times. We don’t really care about substitution rates or how much variation there is in those rates across edges. The rates are just nuisance parameters that must be handled reasonably in order to get at what we really want, the divergence times.

In this lab, we will not be using fossil information to calibrate divergence times. We will assume that the root has age 1.0 and focus on estimating relative divergence times. There are several good tutorials on the RevBayes Tutorials web page that show you how to handle fossil calibration in RevBayes. This tutorial is intended to make you aware of all the issues surrounding divergence time estimation so that you have sufficient background to fully appreciate the tutorials on the RevBayes site.

Let’s continue our example by adding some moves that will modify the tree topology and branching times. Start by making a copy of your relaxed.Rev script, calling the copy divtime.Rev:

cp relaxed.Rev divtime.Rev

Now add the following section just before the section entitled “# Uncorrelated Lognormal relaxed clock”:

# Tree moves

# Add moves that modify all node times except the root node
moves[nmoves++] = mvNodeTimeSlideUniform(timetree, weight=10.0)

# Add several moves that modify the tree topology
moves[nmoves++] = mvNNI(timetree, weight=5.0)
moves[nmoves++] = mvNarrow(timetree, weight=5.0)
moves[nmoves++] = mvFNPR(timetree, weight=5.0) 

Note that we are giving extra weight to these moves, so each tree topology move will be attempted 5 times more often, and the node time slider move will be attempted 10 times more often, than the other moves we’ve defined.

Note also that we’re still starting the MCMC off with the true tree topology and node times (see the line timetree.setValue(T)). This is cheating, of course, but the result would be the same if you started with a maximum likelihood estimate obtained under a strict clock.

Add the following to the very end of the divtime.Rev file (but before quit()). This will read all the sampled trees (each will be different this time because we added moves to modify tree topology and node times) and create a consensus tree showing 95% credible intervals around each divergence time:

# Summarize divergence times

tt = readTreeTrace("output/divtime.trees", "clock")
tt.summarize()
mapTree(tt, "output/divtimeMAP.tre")

Important: Be sure to change all your output files to have the prefix divtime rather than relaxed so that you don’t overwrite the previous results, then run the new model:

rb divtime.Rev

Be prepared to wait for a little longer this time; we’ve added a lot of extra work to the analysis.

Review results of the divergence time analysis

Open the divtime.log file in Tracer.

Also open the divtimeMAP.tre file in FigTree, check the Node Bars checkbox, then specify age_95%HPD for Display after expanding the Node Bars section. You may also wish to use File > New… from the FigTree main menu to open up a new window, then paste the tree description from _trees.txt into the new window for comparison. It also helps to expand the Trees section of FigTree and check the Order nodes checkbox so that both trees are ladderized the same direction.

We’ve added moves, but no parameters or priors for the node times. Why not?

Does the MAP tree have the same topology as the true tree

Are we more confident about recent nodes or ancient nodes in the tree?

What would you conclude if these credible intervals were exactly the same size if we had performed the MCMC analysis on the prior only, with no data?

Obtaining credible intervals under the prior

To finish up the lab, let’s see what the credible interval sizes are under the prior. While we could explore the actual prior, the results would be a little disappointing. For example, under the pure birth model we are using, sampling from the prior would yield many thousands of very different tree topologies, and the consensus of all these disparate trees would be a star tree, which would not be very interesting. Similarly, allowing the birth_rate to be sampled from its prior (which has mean 100 and variance 10000!) would produce trees that, on average, look so different from the tree we used to simulate our data that comparison of divergence time credible intervals would be difficult. So, we will fix the tree topology and birth_rate prior to their true values but keep the ucln_mu, ucln_sigma, and the branch_rates priors at their original values. This means that we will only be looking at the prior on rates, not node times.

Copy your divtime.Rev file to create a new file named divprior.Rev and make the following changes in the new file:

Change output file names to have prefix divprior rather than divtime so that you will not overwrite previous files (don’t forget to do this in the readTreeTrace and mapTree commands);
Comment out the 3 lines setting up moves (mvNNI, mvNarrow, mvFNPR) that change tree topology;

Comment out the 3 existing lines setting up the prior and slide move for birth_rate and replace with a single line making the birth_rate a constant node:

  #birth_rate ~ dnExponential(0.01)
  #birth_rate.setValue(1.0)
  #moves[nmoves++] = mvSlide(birth_rate, delta=1.0, tune=true, tuneTarget=0.4, weight=1.0)
  birth_rate <- 2.6

Change the setup for the mnScreen monitor to have printgen=10000 rather than printgen=100; and
Change the MCMC burnin and run commands to include underPrior=TRUE, and change the number of generations in the run command to 1 million (don’t worry, it goes fast if you don’t ever calculate a likelihood!):
```
  mymcmc.burnin(generations=1000, tuningInterval=100, underPrior=TRUE)
  mymcmc.run(generations=1000000, underPrior=TRUE)
```

Now run the file as usual:

rb divprior.Rev

Open both divpriorMAP.tre and divtimeMAP.tre and make the node bars equal the 95% HPD intervals in each.

Does the data contain information about substitution rates?

Where to continue

If you need to estimate divergence times, and especially if you have fossils that can help you calibrate the molecular clock (so that you don’t have to pin the root time at 1.0 like we did here), you should continue with the tutorial Relaxed Clocks and Time Trees on the RevBayes web site.

What to turn in

Use FigTree to create a PDF figure of your divtimeMAP.tre with credible intervals indicated by bars and send that along with your thinking questions to Analisa on Slack to get credit.