Homework 6

Compute the JC likelihood

The python program below will be modified by you to compute the likelihood of a 4-taxon tree using data from 2 sites. You will check your results using PAUP*.

Be sure to ask for help if you get stuck.

from math import exp, log

# You should *not* modify this function
# same_list holds number of edges with the same state at both ends
# v is the edge length (same for all 5 edges in the tree)
# r is the relative rate
def sitelike(same_list, v, r):
    probsame = 0.25 + 0.75*exp(-4.0*r*v/3.0)
    probdiff = 0.25 - 0.25*exp(-4.0*r*v/3.0)
    like = 0.0
    for n in same_list:
        nsame=float(n)
        ndiff=float(5-n)
        like += 0.25*(probsame**nsame)*(probdiff**ndiff)
    return like

same1 = [5, 2, 2, 2, 2, 1, 0, 0, 2, 0, 1, 0, 2, 0, 0, 1]
same2 = [2, 1, 2, 2, 1, 2, 2, 2, 0, 0, 2, 1, 0, 0, 1, 2]

# Results for JC model
v = 0.1
like1 = sitelike(same1, v, 1.0)
like2 = sitelike(same2, v, 1.0)
print('JC model (brlens = %.1f):' % v)
print(' log-likelihood for site 1 =', log(like1))
print(' log-likelihood for site 2 =', log(like2))
print(' total log-likelihood =', log(like1)+log(like2))
print()

# Results for JC+I model
v = 0.1
pinvar = 0.4
r1 = 0.0
r2 = 1.0/(1.0 - pinvar)
#like1 = pinvar*sitelike(same1, v, r1) + (1.0 - pinvar)*sitelike(same1, v, r2)
#like2 = 
#print('JC+I model (brlens = %.1f, pinvar = %.1f):' % (v,pinvar))
#print(' log-likelihood for site 1 =', log(like1))
# print(' log-likelihood for site 2 =', log(like2))
# print(' total log-likelihood =', log(like1)+log(like2))
#print()

# Results for JC+G model
# v     =
# shape =
# r1    = 
# r2    = 
# r3    = 
# r4    = 
# like1 = 
# like2 = 
# print('JC+G model (brlens = %.1f, shape = %.1f):' % (v,shape))
# print(' log-likelihood for site 1 =', log(like1))
# print(' log-likelihood for site 2 =', log(like2))
# print(' total log-likelihood =', log(like1)+log(like2))
# print()

Ensure that you have access to python3 on the cluster by loading this module:

module load python/3.10.1

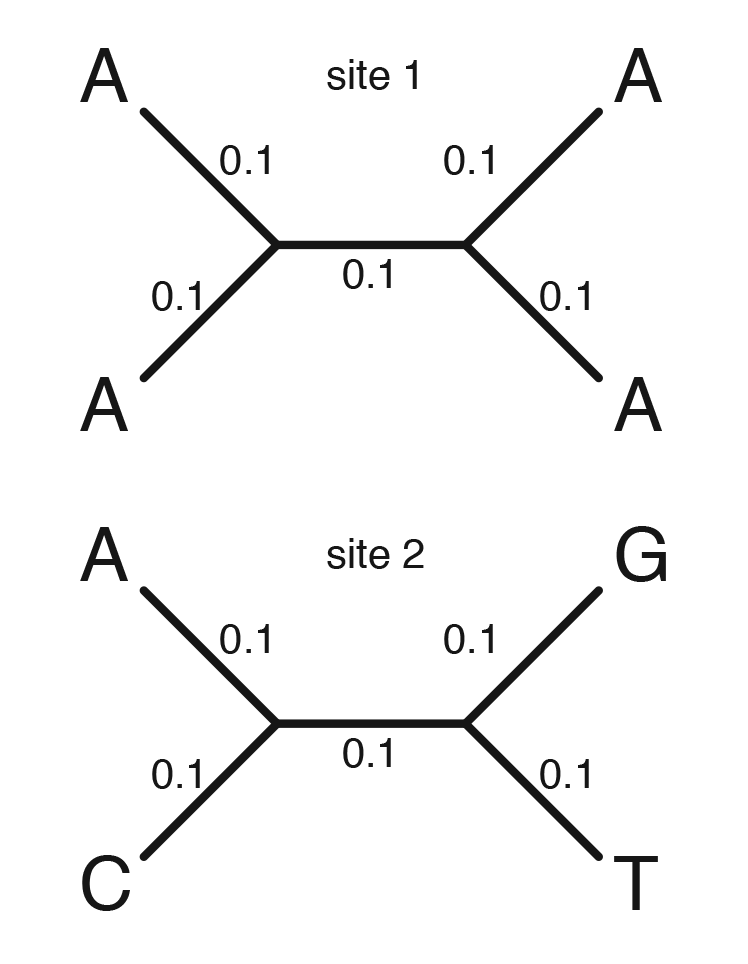
Run this program as follows to compute the site log-likelihoods for the two sites whose data is shown on the tree in Figure 1:

python3 hw6.py

You should see output like that shown below:

JC model (brlens = 0.1):
 log-likelihood for site 1 = -1.8775282342232047
 log-likelihood for site 2 = -9.887165347740401
 total log-likelihood = -11.764693581963606

The sitelike function

Near the top of your hw6.py file is the definition of a function named sitelike. The function sitelike has 3 parameters. The first, same_list, is a list of 16 numbers representing the number of branches (of the 5 total) in which the state is the same at both ends. There are 16 such values because there are 16 possible ancestral state combinations (this should make sense given the homework assignment you did last week).

The second parameter is v, which is the length to be used for all 5 edges (always enter 0.1 for v).

The third and final parameter is r, which is the relative rate to use when computing the site likelihood. Note that r modifies the value of v inside the transition probability formulas. So, to compute the log likelihood for site 1, just pass the list same1 as the first argument when you call the sitelike function. To compute the log likelihood for site 2, pass the list same2 into the function. Note that sitelike function computes the site likelihood, not the logarithm of the site likelihood.

Compute the JC+I likelihood

Now modify your Python program to compute the site log-likelihoods under a JC+I model (proportion of invariable sites = $p_{\mbox{invar}}$ = 0.4).The likelihood for each site must take account of two relative rates: $r_1 = 0.0$ and $r_2 = 1/(1 − p_{\mbox{invar}})$. Note that the function sitelike does all the hard work for you and you will not need to modify it! Pass in the rate you want to use as the last argument to compute the site likelihood given that rate. Here is the general formula for a mixture model with two categories:

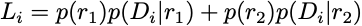
Likelihood for site i

Note that I’ve done like1 for you. Compare that line with the above formula to see how to compute each of the four quantities needed for the site likelihood calculation. You will need to uncomment the lines I’ve commented out and provide the rest of the line beginning like2 =. Your program should print out the two site log-likelihoods and the total log-likelihood as was done for the JC model.

Compute the JC+G likelihood

Modify the Python program again to uncomment the remaining lines in the section labeled “Results for JC+G model” and fill in the code needed to compute the site log-likelihoods under a JC+G model (gamma shape=0.2, 4 categories).

You can use PAUP* to obtain the 4 relative rates. Start PAUP* interactively (i.e. do not specify a file name when starting PAUP*)

module load paup/4.0a-166
paup

and then issue the command

gammaplot shape=0.2 ncat=4

The relative rates that you need are in the right-most column of the table at the end of the output. PAUP* also shows you the boundaries of the 4 categories, but you do not need to use those values.

Checking your answer

You can (and should) check your answer using PAUP*. You can get the data for this homework into PAUP* by creating a nexus file named hw6.nex (see the data block example in the nexus lab). The number of taxa will be 4 and the number of characters will be 2. Create a trees block (see the trees block example in the nexus lab) below your data block containing the tree definition. Finally, add a paup block containing the commands necessary to compute the likelihood under a JC+G model. The lscores command in your paup block should look like this:

lscores 1 / sitelike userbrlen;

Including the option sitelike will tell PAUP* to output not only the overall likelihood but also the site likelihoods. Including the option userbrlen tells PAUP* to use the branch lengths you specified in your tree and not to estimate them (you did specify branch lengths in your tree, didn’t you?).

What do I turn in?

Please email me (paul.lewis@uconn.edu) and attach your python program hw6.py as well as your hw6.nex file to the email.