Homework 7 (MCMC)

Markov chain Monte Carlo (MCMC)

In this homework assignment you will cause a metaphorical “MCMC robot” to move several steps on the landscape shown below. The landscape that your robot will be walking on is the posterior kernel, which is, at every point along the x-axis, the likelihood multiplied by the prior probability density. Because the numbers are so small, we will keep all the calculations on the log scale, in which case the log posterior kernel equals, for every point (edge length), the log prior density plus the log likelihood.

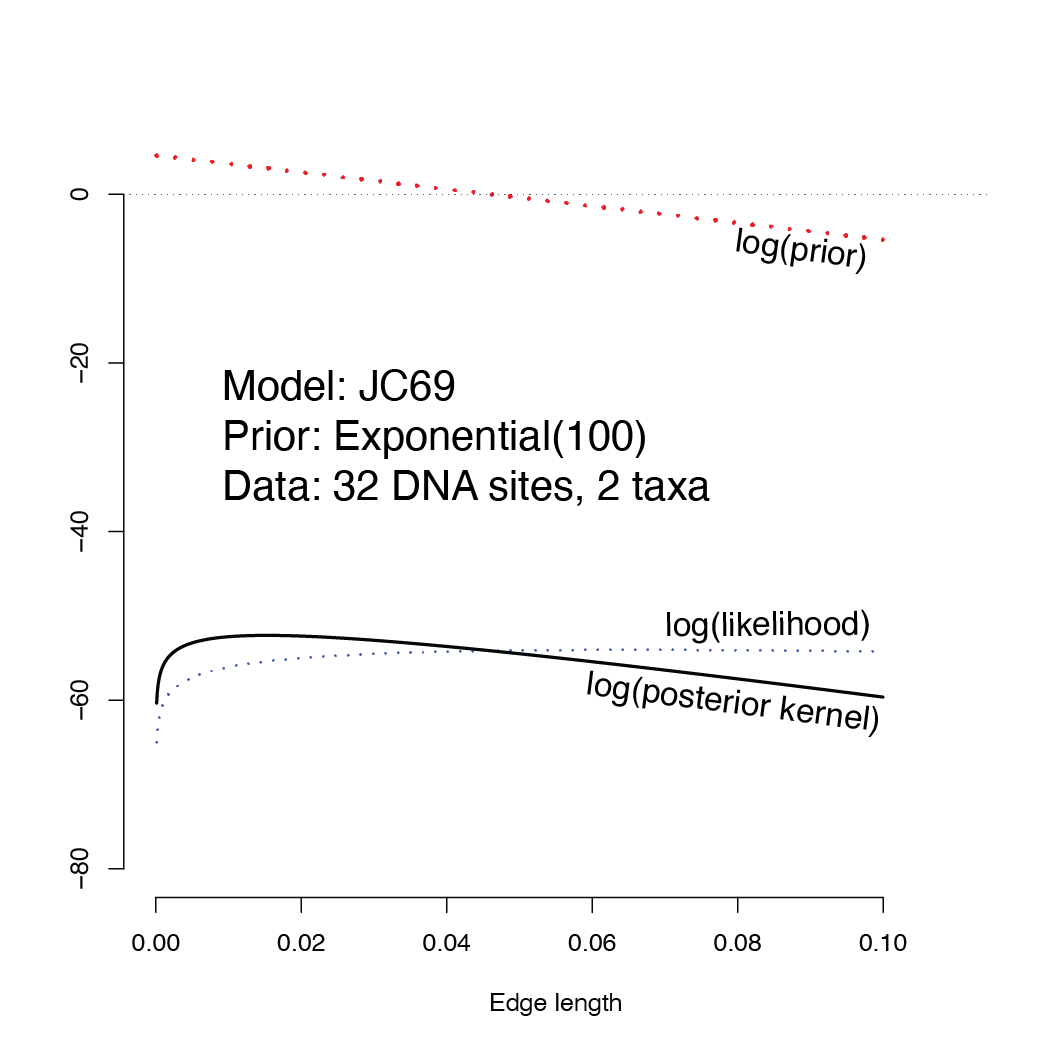
Note how the prior increases toward zero, making the posterior kernel higher than the likelihood for small edge lengths and smaller than the likelihood for larger edge lengths.

You will start your robot at the far right point on this landscape (edge length $v = 0.1$). If your robot is exploring the posterior (kernel), where do you think it will be standing after taking 15 steps? Is it more probable that it will be to the left or to the right of the starting point? You needn’t answer these questions now, but think about them and see, after you finish the homework, whether your intuition was correct.

The data

Here is a very small data set that I’ve used in lecture comprising 32 nucleotide sites from the $\psi \eta$-globin pseudogene for gorilla and orangutan. Asterisks indicate the positions of the 2 differences between these sequences.

gorilla   GAAGTCCTTGAGAAATAAACTGCACACACTGG
orangutan GGACTCCTTGAGAAATAAACTGCACACACTGG
           * *

The model

Use the JC69 model for calculating the likelihood, and let the prior for the single parameter $v$ be Exponential(100). The prior probability density for any particular value of $v$ is thus

\[p(v) = 100 e^{-100 v},\]

which means that the log prior density is

\[\log p(v) = \log(100) - 100 v.\]

Important! Be careful to use natural logarithms for these calculations. The natural logarithm of $2.71828183$ will be 1, whereas the common logarithm (base 10) of $2.71828183$ is about 0.4343, so use this fact to check to ensure you are using the correct logarithm function on your calculator, python, R, etc.). In most calculators, you must use the ln function to get natural logarithms; the log function calculates the common logarithm. Python and R both use log to mean natural logarithm and use log10 to compute common logarithms.

Starting point

Start your MCMC “robot” at the value $v=0.1$.

Proposal distribution

To propose a new value $v'$ (given current value $v$) for your MCMC robot to consider, use a sliding window of width 0.05 centered over the current value of $v$.

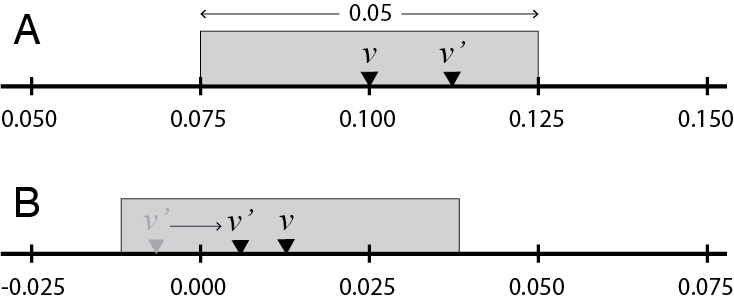
In part A of the figure above, given current value $v = 0.1$ and uniform deviate $u_1 = 0.75$, the proposed new value $v'$ lies 75% of the way across the proposal window (starting from the left end). The proposed value would thus be

\[v' = 0.075 + (0.75)(0.05) = 0.1125.\]

The value 0.075 above is equal to the starting value (0.100) minus half the width of the sliding window (0.025).

Negative proposed values are reflected back into the positive half of the real line. In part B of the figure, the current value is $v = 0.0125$ and the uniform deviate $u_1 = 0.125$, so the proposed new value is

\[v' = −0.0125 + (0.125)(0.05) = −0.00625.\]

This proposed value is negative, and is therefore not a valid value for an edge length, so reflect it back into the valid range by multiplying by -1, yielding $v' = 0.00625.$

What do I turn in?

Please turn in the filled-in worksheet (link to PDF file below) or email/Slack me (paul.lewis@uconn.edu) a photo of the filled in worksheet.

Worksheet in PDF format

Note that you should start by writing in 0.1 in the $v$ column for the row corresponding to iteration 1.

What to do

Each line of the worksheet corresponds to a step taken by your MCMC robot. For each iteration, you will have a starting edge length $v$ (this will be 0.1 for the first iteration) and will need to propose a new value $v'$ using uniform random deviate $u_1$. You will then compute the log of the acceptance ratio $R$ and use uniform random deviate $u_2$ to decide whether to accept the proposed value $v'$ or keep the original value $v$. If you accept the proposed new edge length, then you will use that value as your starting value for the next iteration; if you reject the proposed new edge length, then the next iteration will start with the same value as the current iteration. Note that you will accept $v’$ if $\log(u_2) < \log(R)$ (this is equivalent to asking whether $u_2 < R$).

Python helper program

If the python script below is saved as hw7.py, it can be called like this:

python3 hw7.py 0.05

The hw7.py script will compute the log-likelihood, log-prior-density, and log-posterior-kernel for the supplied edge length (i.e. the 0.05 in python3 hw7.py 0.05).

import math, random, sys

def logLikelihood(v):
    logsame = 2.0*math.log(0.25) + math.log(1.0 + 3.0*math.exp(-4.0*v/3.0))
    logdiff = 2.0*math.log(0.25) + math.log(1.0 - math.exp(-4.0*v/3.0)) 
    return (2.0*logdiff + 30.0*logsame)
    
def logPrior(v):
    exponential_rate = 100.0
    return (math.log(exponential_rate) - v*exponential_rate)
    
def logPosteriorKernel(v):
    return (logLikelihood(v) + logPrior(v))
        
v = float(sys.argv[1])
print('v                     = %12.5f' % v)
print('log(likelihood)       = %12.5f' % logLikelihood(v))
print('log(prior)            = %12.5f' % logPrior(v))
print('log(posterior kernel) = %12.5f' % logPosteriorKernel(v))

Thus, the hw7.py program will calculate every quantity you need except for the proposed edge length. The uniform random variates you need to choose the proposed edge length given the current edge length are provided (so that you will get the same answer as me, making it much easier for me to grade!).

Even though hw7.py spits out the log-likelihood and log-prior, the only quantity you need is the log-posterior-kernel. The posterior kernel is the height of the “landscape” that the “robot” is exploring.

Note that $\log(R)$ equals the log-posterior-kernel of the proposed edge length minus the log-posterior-kernel of the current point. The value of $\log(R)$ will be negative if the “robot” is proposing to go downhill and will be positive if it is proposing to go uphill.