BayesTraits Lab
Up to the Phylogenetics main page
Goals
In this lab you will learn how to use the program BayesTraits, written by Andrew Meade and Mark Pagel. BayesTraits can perform several analyses related to evaluating evolutionary correlation and ancestral state reconstruction in discrete morphological traits.
Lab answer worksheet
Copy the following text into a text file and use this template to answer the 
questions along the way.
1. Which occurs at a faster rate: pinnate to palmate, or palmate to pinnate?
answer:
2. Which occurs at a faster rate: entire to dissected, or dissected to entire?
answer:
3. What type of joint evolutionary transitions seem to often have very low rates (look for an abundance of zeros in a column)?
answer:
4. What type of joint evolutionary transitions seem to often have very high rates (look for columns with rates in the hundreds)?
answer:
5. Why am I suggesting this switch? (Hint: what is the support of a Uniform(0,100) distribution vs. an Exponential(1/29) distribution?)
answer:
6. Why choose 29? (Hint: the variance of a Uniform(0,100) distribution equals 100^2/12 and the variance of an Exponential(1/29) distribution equals 29^2)
answer:
7. What is the log marginal likelihood estimated using the stepping-stone method? This value is listed on the last line of the file _mcmc-dependent.Stones.txt_
answer:
8. What is the estimated log marginal likelihood for this analysis using the stepping-stone method?
answer:
9. Which is the better model (dependent or independent) according to these estimates of marginal likelihood?
answer:
10. Which model string is most common?
answer:
11. What does this model imply?
answer:
12. So what is the estimated marginal posterior probability that q21=0?
answer:
13. Why is the term marginal appropriate here (as in marginal posterior probability)?
answer:
14. Which state is most common at the xerophyte MRCA node for leaf venation?
answer:
15. Which state is most common at the xerophyte MRCA node for leaf dissection?
answer:
Getting started
Login to your account on the Health Center (Xanadu) cluster, then issue
srun --qos=mcbstudent --partition=mcbstudent --mem=1G --pty bash
to start a session on a node that is not currently running jobs.
Create a directory
Use the unix mkdir command to create a directory to play in today:
mkdir ~/btlab
cd ~/btlab
Download BayesTraits
There is no module for BayesTraits, so we will have to download the latest version into your home directory:
curl -O https://www.evolution.reading.ac.uk/BayesTraitsV4.1.1/Files/BayesTraitsV4.1.1-Linux.tar.gz
Now unpack the gzipped “tape archive” (tar) file as follows:
tar zxvf BayesTraitsV4.1.1-Linux.tar.gz
This will create a directory named BayesTraitsV4.1.1-Linux in your home directory. Move the BayesTraits executable from inside BayesTraitsV4.1.1-Linux down one level to your home directory for easier access:
cd BayesTraitsV4.1.1-Linux
mv BayesTraitsV4 ..
cd ..
The third line above (cd ..) should move you back to the ~/bdlab directory. Check this using the pwd command:
pwd
Go back to Mark Pagel’s web site and download the manual for BayesTraits. This is a PDF file and should open in your browser window.
A little aside on tar files
Data used to be stored on magnetic tape, not hard drives, and the tar (tape archive) program is what was used to move files to and from the tape. This tells you something about how old the tar format is because perhaps none of you have even seen a magnetic tape used for data storage! The tar command takes all the files in a directory and simply concatenates them into one gigantic file. It also preserves file permissions and the directory structure. The four letters after the command name tar are zxvf. These stand for the following:
- z = uncompress (the gz at the end of the file tells you it is a compressed archive, so the z tells tar to uncompress it before unpacking it)
- x = extract (unpack the archive into individual files. You would use c here if you were creating a tar file)
- v = verbose (tell us what’s going on as you unpack)
- f = file (this tells tar that the file name is coming next, so don’t put f earlier in the list)
This tar file has been compressed using the program gzip, which adds the gz ending to the file name. Most tar files are compressed with gzip or some similar algorithm so that the file requires less time to move across the internet.
Download the tree and data files
For this exercise, you will use data and trees used in the SIMMAP analyses presented in this paper:
Jones C.S., Bakker F.T., Schlichting C.D., Nicotra A.B. 2009. Leaf shape evolution in the South African genus _Pelargonium_ L'Her. (Geraniaceae). Evolution. 63:479–497.
The data and trees were not made available in the online supplementary materials for this paper, but I have obtained permission to use them for this laboratory exercise.
pelly.txt This is the data file. It contains data for two traits (leaf dissection and leaf venation) for 154 taxa in the plant genus Pelargonium.
pelly.tre This is the tree file. It contains 99 trees sampled from an MCMC analysis of DNA sequences.
Here’s how to curl these files into your btlab folder
curl -O https://plewis.github.io/assets/data/pelly.txt
curl -O https://plewis.github.io/assets/data/pelly.tre
Assessing the strength of association between two binary characters
The first thing we will do is see if the two characters (leaf dissection and leaf venation) in pelly.txt are evolutionarily correlated.
Trait 1: Leaf dissection
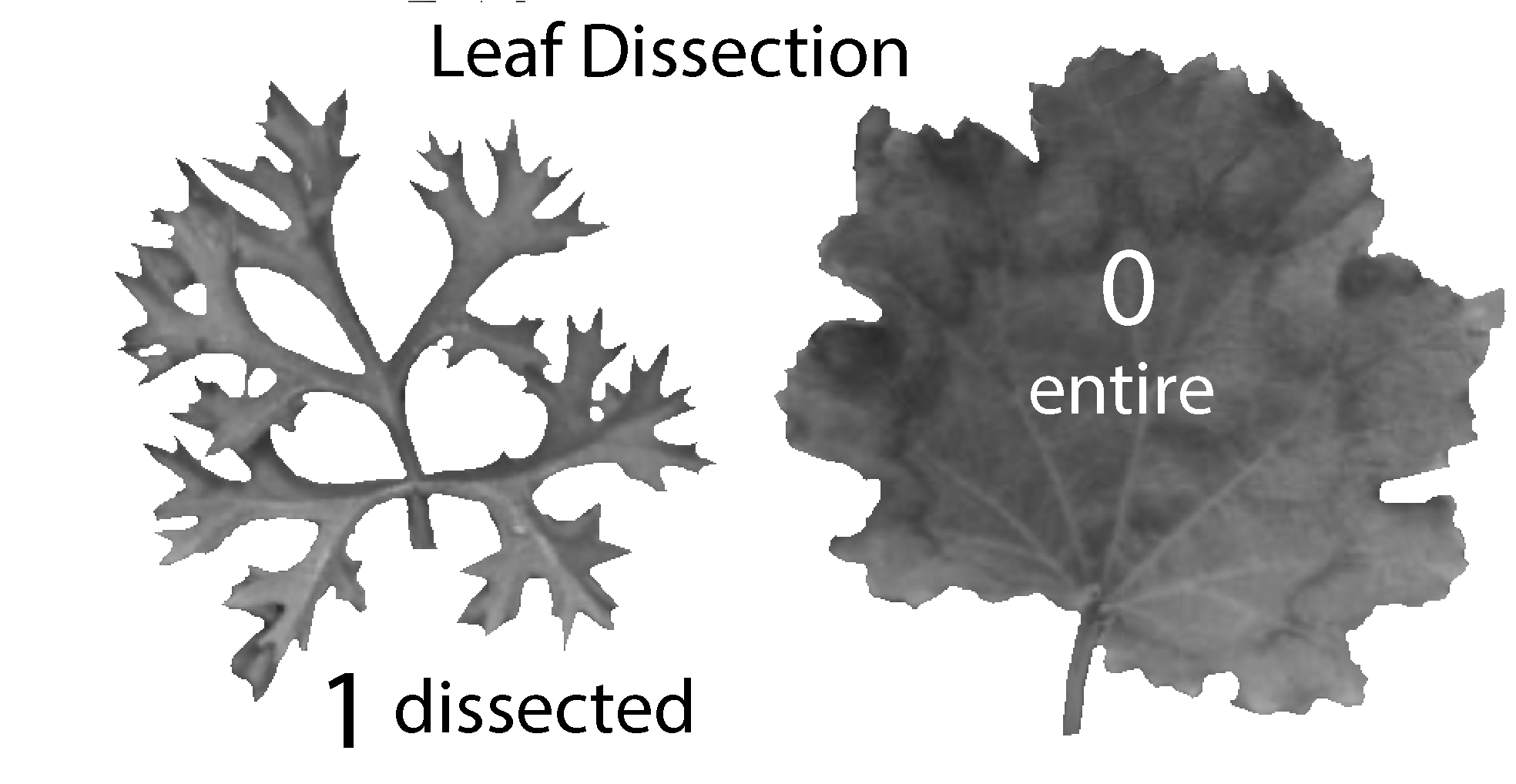
The leaf dissection trait comprises two states (I’ve merged some states in the original data matrix to produce just 2 states):
- 0 means leaves are entire (unlobed or shallowly lobed in the original study), and
- 1 means leaves are dissected (lobed, deeply lobed, or dissected in the original study).
Trait 2: Leaf venation
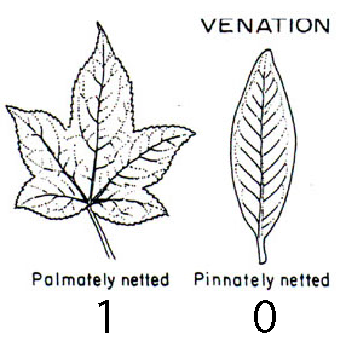
The leaf venation trait comprises two states:
- 0 means leaves are pinnately veined (one main vein runs down the long axis of the leaf blade), and
- 1 means leaves are palmately veined (several major veins meet at the base of the leaf).
We will first use maximum likelihood to estimate the rates at which these two traits evolve under both an independent model (traits assumed to evolve independently) and a dependent model (the rates of change in one trait may differ depending on the state present in the other trait).
To test whether these two traits are correlated, we will carry out Bayesian MCMC analyses and estimate the marginal likelihood under two models. The model (independent or dependent) with the higher marginal likelihood will be the preferred model. You will recall that we discussed both of these models in lecture, and also discussed the stepping-stone method that BayesTraits uses to evaluate models. You may wish to pull up those lectures to help answer the questions that you will encounter momentarily, as well as the BayesTraits manual.
Then we will use reversible-jump MCMC to determine which of several thousand models is best. This method effectively uses marginal likelihoods to choose among models, but has the advantage that you need not specify which models you are interested in comparing beforehand.
Finally, I’ll show you how to estimate the marginal posterior probabilities of different ancestral state combinations using BayesTraits.
Maximum Likelihood: Independence model
Type the following to start the BayesTraits program (assuming you are in the btlab folder):
./BayesTraitsV4 pelly.tre pelly.txt
You should see this selection appear:
Please select the model of evolution to use.
1) MultiState
2) Discrete: Independent
3) Discrete: Dependant
4) Continuous: Random Walk (Model A)
5) Continuous: Directional (Model B)
6) Continuous: Regression
7) Independent Contrast
8) Independent Contrast: Correlation
9) Independent Contrast: Regression
10) Discrete: Covarion
12) Fat Tail
13) Geo
Press the 2 key and hit enter to select the Independent model. Now you should see these choices appear:
Please Select the analysis method to use.
1) Maximum Likelihood.
2) MCMC
Press the 1 key and hit enter to select maximum likelihood. Now you should see some output showing the choices you explicitly (or implicitly) made:
Options:
Model: Discrete: Independent
Tree File Name: pelly.tre
Data File Name: pelly.txt
Log File Name: pelly.txt.Log.txt
Save Initial Trees: False
Save Trees: False
Summary: False
Seed: 664656726
Analsis Type: Maximum Likelihood
ML Attempt Per Tree: 10
ML Max Evaluations: 20000
ML Tolerance: 0.000001
ML Algorithm: BOBYQA
Rate Range: 0.000000 - 100.000000
Precision: 64 bits
Cores: 1
No of Rates: 4
Base frequency (PI's): None
Pis used in ancestral state estimation: Yes
Character Symbols: 00,01,10,11
Using a covarion model: False
Normalise Q Matrix: False
Restrictions:
alpha1 None
beta1 None
alpha2 None
beta2 None
Tree Information
Trees: 99
Taxa: 154
Sites: 1
States: 4
Now type run and hit enter to perform the analysis, which will consist of estimating the parameters of the independent model on each of the 99 trees contained in the pelly.tre file. You will notice that BayesTraits created a new file: pelly.txt.Log.txt.
Rename this file ml-independent.txt so that it will not be overwritten the next time you run BayesTraits:
mv pelly.txt.Log.txt ml-independent.txt
Open the ml-independent.txt file in nano (or bring it back to your laptop and use BBEdit (Mac) or Notepad++ (Windows) to view it). Scrolling past the first 33 lines, you should see the start of the parameter samples:
Tree No Lh alpha1 beta1 alpha2 beta2 Root - P(0,0) Root - P(0,1) Root - P(1,0) Root - P(1,1)
1 -157.362972 53.767527 34.523176 35.319157 20.707416 0.249998 0.250002 0.249998 0.250002
2 -158.179984 53.313539 34.182683 36.038859 20.997536 0.249999 0.250001 0.249999 0.250001
.
.
.
98 -156.647307 52.357626 36.749282 27.270771 13.086248 0.250244 0.249756 0.250244 0.249756
99 -156.532925 52.321467 36.641688 27.402067 13.200124 0.250234 0.249767 0.250233 0.249766
(Optional: download the ml-independent.txt file to your laptop, use a text editor to strip the first 33 lines, and open the file in Tracer.)
Answer these questions using the output you have generated. Here’s a key to the meaning of each column in the file:
| Column | Description |
|---|---|
| Tree No | Tree from pelly.tre |
| Lh | log-likelihood |
| alpha1 | leaf dissection: rate 0 (entire) -> 1 (dissected) |
| beta1 | leaf dissection: rate 1 (dissected) -> 0 (entire) |
| alpha2 | leaf venation: rate 0 (pinnate) -> 1 (palmate) |
| beta2 | leaf venation: rate 1 (palmate) -> 0 (pinnate) |
| Root - P(0,0) | prob. state 0,0 at root node |
| Root - P(0,1) | prob. state 0,1 at root node |
| Root - P(1,0) | prob. state 1,0 at root node |
| Root - P(1,1) | prob. state 1,1 at root node |
Maximum Likelihood: Dependence model
Run BayesTraits again, this time typing 3 on the first screen to choose the dependence model and again typing 1 on the second screen to select maximum likelihood. You should see this output showing the options selected:
Options:
Model: Discrete: Dependent
Tree File Name: pelly.tre
Data File Name: pelly.txt
Log File Name: pelly.txt.Log.txt
Save Initial Trees: False
Save Trees: False
Summary: False
Seed: 776907455
Analsis Type: Maximum Likelihood
ML Attempt Per Tree: 10
ML Max Evaluations: 20000
ML Tolerance: 0.000001
ML Algorithm: BOBYQA
Rate Range: 0.000000 - 100.000000
Precision: 64 bits
Cores: 1
No of Rates: 8
Base frequency (PI's): None
Pis used in ancestral state estimation: Yes
Character Symbols: 00,01,10,11
Using a covarion model: False
Normalise Q Matrix: False
Restrictions:
q12 None
q13 None
q21 None
q24 None
q31 None
q34 None
q42 None
q43 None
Tree Information
Trees: 99
Taxa: 154
Sites: 1
States: 4
Run the analysis. Here is an example of the output produced (in the file pelly.txt.Log.txt) after you type run to start the analysis:
Tree No Lh q12 q13 q21 q24 q31 q34 q42 q43 Root - P(0,0) Root - P(0,1) Root - P(1,0) Root - P(1,1)
1 -151.930254 66.451053 37.783888 0.000000 62.220033 23.997490 23.299393 46.110432 36.632979 0.24999 0.249981 0.250026 0.250000
2 -152.925691 67.152271 38.611193 0.000000 60.925185 24.514488 23.937433 45.313366 37.199310 0.24999 0.249983 0.250023 0.250001
.
.
.
98 -150.816306 36.534843 27.359325 0.000000 66.563262 19.823546 24.944519 63.940577 31.074092 0.250048 0.249750 0.250304 0.249898
99 -150.712705 37.316351 27.260833 0.000000 64.364694 20.107653 25.004246 60.945163 31.658536 0.250030 0.249779 0.250272 0.249919
Before doing anything else, rename the file pelly.txt.Log.txt to ml-dependent.txt so that it will not be overwritten the next time you run BayesTraits.
mv pelly.txt.Log.txt ml-dependent.txt
Here’s a key to the rates:
| Rate | Context | Transition |
|---|---|---|
| q12 | dissection: 0 (entire) | venation: 0 (pinnate) -> 1 (palmate) |
| q13 | venation: 0 (pinnate) | dissection: 0 (entire) -> 1 (dissected) |
| q21 | dissection: 0 (entire) | venation: 1 (palmate) -> 0 (pinnate) |
| q24 | venation: 1 (palmate) | dissection: 0 (entire) -> 1 (dissected) |
| q31 | venation: 0 (pinnate) | dissection: 1 (dissected) -> 0 (entire) |
| q34 | dissection: 1 (dissected) | venation: 0 (pinnate) -> 1 (palmate) |
| q42 | venation 1 (palmate) | dissection: 1 (dissected) -> 0 (entire) |
| q43 | dissection: 1 (dissected) | venation: 1 (palmate) -> 0 (pinnate) |
Bayesian MCMC: Dependence model
Run BayesTraits again, typing 3 on the first screen to choose the dependence model and this time typing 2 on the second screen to select MCMC. You should see this output showing the options selected:
Options:
Model: Discrete: Dependent
Tree File Name: pelly.tre
Data File Name: pelly.txt
Log File Name: pelly.txt.Log.txt
Save Initial Trees: False
Save Trees: False
Summary: False
Seed: 1326361449
Precision: 64 bits
Cores: 1
Analysis Type: MCMC
Sample Period: 1000
Iterations: 1010000
Burn in: 10000
MCMC ML Start: False
Schedule File: pelly.txt.Schedule.txt
Rate Dev: AutoTune
No of Rates: 8
Base frequency (PI's): None
Pis used in ancestral state estimation: Yes
Character Symbols: 00,01,10,11
Using a covarion model: False
Normalise Q Matrix: False
Restrictions:
q12 None
q13 None
q21 None
q24 None
q31 None
q34 None
q42 None
q43 None
Prior Information:
Prior Categories: 100
Priors
q12 - uniform 0.00 100.00
q13 - uniform 0.00 100.00
q21 - uniform 0.00 100.00
q24 - uniform 0.00 100.00
q31 - uniform 0.00 100.00
q34 - uniform 0.00 100.00
q42 - uniform 0.00 100.00
q43 - uniform 0.00 100.00
Tree Information
Trees: 99
Taxa: 154
Sites: 1
States: 4
Before typing run type the following command, which tells BayesTraits to change all priors from the default Uniform(0,100) to an Exponential distribution with mean 29:
pa exp 29
Also type the following to ask BayesTraits to perform a stepping-stone analysis:
stones 100 10000
Now run the analysis. This will estimate 100 ratios to brook the gap between posterior and prior, using a sample size of 10000 for each “stone”.
Here is an example of the output stored in the file pelly.txt.Log.txt after you type run to start the analysis:
Iteration Lh Tree No q12 q13 q21 q24 q31 q34 q42 q43 Root - P(0,0) Root - P(0,1) Root - P(1,0) Root - P(1,1)
11000 -155.195365 78 14.423234 34.800270 8.845985 45.927148 12.622435 50.476188 52.844895 32.149168 0.250068 0.249969 0.249994 0.249968
12000 -154.161705 82 64.601017 12.382781 9.259134 51.796365 12.002095 23.744903 30.316089 21.865930 0.249936 0.249957 0.250095 0.250012 .
.
.
1009000 -154.343996 30 33.555198 50.086092 11.294490 38.518607 24.461032 47.295157 43.477964 21.726938 0.250057 0.249939 0.250045 0.249959
1010000 -154.195259 87 29.584898 35.410909 2.003582 61.981073 16.976124 14.895266 49.111354 14.419644 0.251115 0.247854 0.252551 0.248480
Before doing anything else, rename the file pelly.txt.Log.txt to mcmc-dependent.txt, and pelly.txt.Stones.txt to mcmc-dependent.Stones.txt so that they will not be overwritten the next time you run BayesTraits.
mv pelly.txt.Log.txt mcmc-dependent.txt
mv pelly.txt.Stones.txt mcmc-dependent.Stones.txt
The Tree No column shows which of the 99 trees in the supplied pelly.tre treefile was chosen at random to be used for that particular sample point. BayesTraits is sampling trees from the posterior distribution here; it cannot actually sample trees from the posterior because we have given it only data for two morphological characters, which would not provide nearly enough information to estimate the phylogeny for 154 taxa. It is as if we had given BayesTraits sequence data as well as our 2 morphological characters and it was using only the sequence data to estimate the posterior distribution of trees and edge lengths and only the morphological data to estimate rates for the morphological characters.
Try to answer these questions using the output you have generated:
Bayesian MCMC: Independence model
Run BayesTraits again, this time specifying the Independent model, and again using MCMC, pa exp 29, and stones 100 10000. Rename the output file from pelly.txt.log.txt to mcmc-independent.txt. Also rename pelly.txt.Stones.txt to mcmc-independent.Stones.txt:
mv pelly.txt.Log.txt mcmc-independent.txt
mv pelly.txt.Stones.txt mcmc-independent.Stones.txt
Bayesian Reversible-jump MCMC
Run BayesTraits again, specifying Dependent model, MCMC and, this time, specify the reversible-jump approach using the command
rj exp 29
The previous command also sets the prior. Type run to start, then when it finishes rename the output file rjmcmc-dependent.txt:
mv pelly.txt.Log.txt rjmcmc-dependent.txt
The reversible-jump approach carries out an MCMC analysis in which the number of model parameters (the dimension of the model) potentially changes from one iteration to the next. The full model allows each of the 8 rate parameters to be estimated separately, while other models restrict the values of some rate parameters to equal the values of other rate parameters. The output contains a column titled Model string that summarizes the model in a string of 8 symbols corresponding to the 8 rate parameters q12, q13, q21, q24, q31, q34, q42, and q43. For example, the model string “‘1 0 Z 0 1 1 0 2” sets q21 to zero (Z), q13=q24=q42 (parameter group 0), q12=q31=q34 (parameter group 1), and q43 has its own non-zero value distinct from parameter groups 0 and 1.
You could copy the “spreadsheet” part of the output file into Excel and sort by the model string column, but let’s instead use Python to summarize the output file. Download (e.g. using curl) the file btsummary.py and run it as follows:
curl -O https://plewis.github.io/assets/scripts/btsummary.py
module load python/3.8.1
python3 btsummary.py
This should produce counts of model strings. (If it doesn’t, check to make sure your output file is named rjmcmc-dependent.txt because btsummary.py tries to open a file by that name.) Answer the following questions using the counts provided by btsummary.py:
Notice that many (but not all) model strings have Z for q21. One way to estimate the marginal posterior probability of the hypothesis that q21=0 is to sum the counts for all model strings that have Z in that third position corresponding to q21. While it is pretty easy to add these numbers in your head, let’s modify btsummary.py to do this for us (this might come in useful if you ever encounter results that are more complex): open btsummary.py in nano and locate the line containing the regular expression search that pulls out all the model strings from the BayesTrait output file:
model_list = re.findall("'[Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9]", stuff, re.M | re.S)
The re.findall function performs a regular expression search of the text stored in the variable stuff looking for strings that have a series of 8 space-separated characters, each of which is either the character Z or a digit between 0 and 9 (inclusive). Copy this line (in nano, you can do this with Ctrl-K (cut), Ctrl-U (uncut), Ctrl-U (uncut)), then comment out one copy by starting the line with the hash (#) character:
#model_list = re.findall("'[Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9]", stuff, re.M | re.S)
model_list = re.findall("'[Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9]", stuff, re.M | re.S)
Now modify the uncommented copy such that it counts only models with Z in the third position of the model string.
model_list = re.findall("'[Z0-9] [Z0-9] Z [Z0-9] [Z0-9] [Z0-9] [Z0-9] [Z0-9]", stuff, re.M | re.S)
Rerun btsummary.py, and now the total matches should equal the number of model strings sampled in which q21=0.
Estimating ancestral states
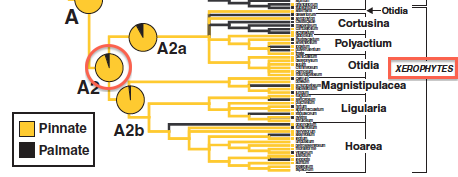
The Jones et al. 2009 study estimated ancestral states using SIMMAP. In particular, they found that the most recent common ancestor (MRCA) of the xerophytic (dry-adapted) clade of pelargoniums almost certainly had pinnate venation (see red circle in figure on right). Let’s see what BayesTraits says.
Start BayesTraits in the usual way, specifying 1 (Multistate) on the first screen and 2 (MCMC) on the second. After the options are output, type the following commands in, one line at a time, finishing with the run command:
pa exp 29
addtag xerotag alternans104 rapaceum130
addmrca xero xerotag
run
The addmrca command tells BayesTraits to add columns of numbers to the output that display the probabilities of each state for each character in the most recent common ancestor of the taxa listed in the addtag command (2 taxa are sufficient to define the MRCA, but more taxa may be included). The column headers for the last four columns of output should be (I’ve added the comments starting with <--)
xero - S(0) - P(0) <-- character 0 (dissection), probability of state 0 (entire)
xero - S(0) - P(1) <-- character 0 (dissection), probability of state 1 (dissected)
xero - S(1) - P(0) <-- character 1 (venation), probability of state 0 (pinnate)
xero - S(1) - P(1) <-- character 1 (venation), probability of state 1 (palmate)
You can download the output file (pelly.txt.Log.txt) and view it in Tracer. That way you can use Tracer to tell you the means of the four columns above. Note that you will need to remove the initial text from the file (but keep the column headers) before Tracer will recognize it.
That concludes the introduction to BayesTraits. A glance through the manual will convince you that there is much more to this program than we have time to cover in a single lab period, but you should know enough now to explore the rest on your own if you need these features.
What to turn in
Send your answers to the thinking questions to Analisa via Slack.